はじめに¶
ただいま確率過程について勉強中なのだが,式展開に疲れたのでさっと「一般Wiener過程」のサンプルパスを作成してみた.
確率過程全般に関する記事は,改めて書きたいと思う.(火傷しそうで怖いけど)
一般Wiener過程¶
一般Wiener過程とは,以下の式で表される確率過程のこと.
$$ \delta x = a \delta t + b \epsilon \sqrt{\delta t} $$ 状態変数$x$の微小時間 $ \delta t$での変位 $ \delta x$ は,右辺第一項トレンドと第二項ボラティリティからなる.
ここで,$a$,$b$はパラメータ(定数)であり,確率界隈ではそれぞれドリフト係数,拡散係数などと呼んだりする.$\epsilon$は正規分布$N(0,1)$に従うノイズである.
なぜ$ \sqrt{\delta t}$なんてものがでてくるのか,なぜこのような式が導出されるのか,
不思議なことはいっぱいだが,その解説をここに示すには余白が狭すぎる.
とりあえず今回はサンプルパスを作成して満足する.
- 参考文献
訳本もでている
実装¶
さっそく実装していく.
In [1]:
#import
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
In [2]:
#さきほどの式にそのまま対応する関数を作成
def dx(a,b,dt):
e = np.random.normal(0,1)
return a*dt + b * e * np.sqrt(dt)
In [3]:
#微小時間幅を設定
dt = 0.1
#時系列tを作成(今回は[0,100]の範囲)
t_list = np.arange(0,100,dt)
#ドリフト係数
a = 0
#拡散係数
b = 1
In [4]:
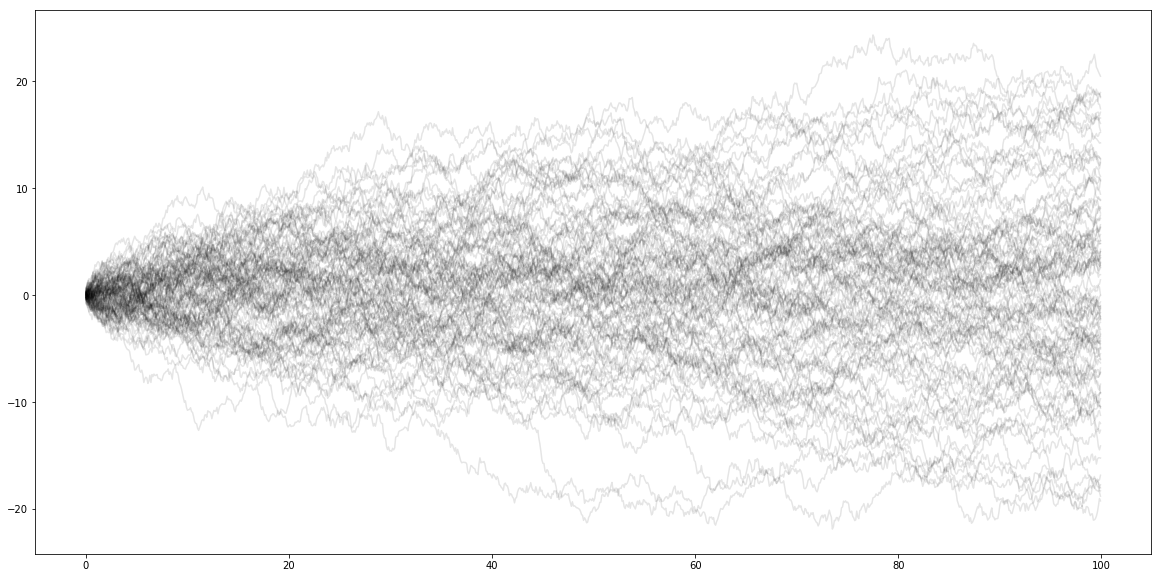
#100サンプルパスを描画してみる
plt.figure(figsize=(20,10))
for i in range(100):
#まずdxのりストを作成し
dx_list = np.array([dx(a,b,dt) for k in range(int(100/dt))])
#状態変数xの時系列は,その累積和で表現(つまりx(0)=0)
#累積和はcumsum()関数を使用
x_list = dx_list.cumsum()
#描画
#alphaは線濃度を指定する引数
plt.plot(t_list, x_list, color="black", alpha=0.1)
In [5]:
#ドリフト係数
a = 1
#100サンプルパスを描画してみる
plt.figure(figsize=(20,10))
for i in range(100):
dx_list = np.array([dx(a,b,dt) for k in range(int(100/dt))])
x_list = dx_list.cumsum()
plt.plot(t_list, x_list, color="black", alpha=0.1)
plt.plot(t_list, a*t_list, color="red", label=r"y=ax")
plt.legend()
Out[5]:
赤線がトレンド項を表す.なんとなく,赤線のまわりにまとわりついているように見えるが,時間が経つにつれだんだんと滲んでくるのがわかる.
この滲みは時刻$t$における確率変数$x$の分散として,数学的に記述できるが今回は割愛.
この滲みは時刻$t$における確率変数$x$の分散として,数学的に記述できるが今回は割愛.
おわりに¶
数式もコード書いた方がイメージが掴める派なので,今後も数学とプログラムを対応させて勉強していきたい.